Mootools Transitions explained

An in-depth tutorial about Mootools Transitions

Usually when using an effect I used to try out possible transitions one after another until I found the right one, but this got quite boring after some time, so I looked at the mootools source code to understand the logic behind – that’s what this tutorial is about.

General information can be found here: mootools.net/docs/core/Fx/Fx.Transitions » and also here: ryanflorence.com/mootools-fx-transitions-demo/ »

What is a transition?

The process or a period of changing from one state or condition to another.

This is the dictionary definition — in our case, when using transitions for Mootols Effects this means the process of changing (element-)values from a beginning state to an ending state.

The example

So as an example let’s use Fx.Tween to change the element width from 50px to 550px in 1 second. Here are several examples of transitions – trigger them by clicking the pink boxes.

If the demo doesn’t work: Reload the page, this should help (or write a comment if the problem persists).

Trigger all » | Reset all »

How to use transitions

This should be nothing new, here the javascript I used for the examples above:

$('element').addEvent('mousedown', function(event) {
	this.set('tween', {duration: 'long', transition: 'cubic:in'});
	this.tween('width', [50, 550]);
});

Alternatively you can write the transition with its classname:

transition: Fx.Transitions.Cubic.EaseIn

Which notation you use is up to you – if you use the string representation, mootools automatically finds the appropriate Fx.Transitions-class.

Elements of a transition

Mootools transitions consist of three elements:

• Duration
• Type of transition
• An additional ease-value (if the type is not linear)

In our example the transition takes the element width and transforms it from the starting value 50 to the target value 500 in one second. The type decides how the in-between values are being calculated, the ease decides from which direction the formula is applied – more about this later on.

Duration

This is simply the duration is it takes to change the values – in microseconds, so a duration of 1000 equals 1 second.

There are three predefined durations:

How are transitions calculated?

Let’s use the above example, the width of an element is being tweened from 50 to 550 pixel, with a duration of 1000 ms. So our starting value from is 50, the target value to is 550. That means we’ve got to cover a distance of 500 pixels in one second.

Now let’s say our transition is expressed as a function f(x), this is the code used in mootools:

This is the mathematical notation, the mootools source code looks more javascript-like of course.

(current_time – starting_time) = the number of milliseconds since the effect was started

The argument of the function is time difference divided by duration – at the beginning this is about 0.0, after 500 ms this value is 0.5, at the end its approximately 1.0. So the transition function is applied to a range from 0.0 to 1.0 (normalized).

Let’s assume we use a linear transition, so f(x) = x:
So the new_value (our new width) is 0.0 to 1.0 times the range (500) plus the initial value (50). Or: At the beginning the width is set to 50 (initial value), after half the time we’ve got 500*0.5+50 = 300, and at the end 500*1.0+50 = 550.

In this case the values from 50 to 500 are distributed uniformly along the unit interval from 0.0 to 1.0 — a linear function.

Types of Transitions

These are: Linear, Quad, Cubic, Quart, Quint, Pow, Expo, Circ, Sine, Back, Bounce and Elastic. Now I’ll explain how they work.

Linear Transition

A linear transition has no additional ease-parameter, since it simply divides the range equally along the timeline, as seen above.

Polynomial (xⁿ) Transitions

In this category we’ve got: Quad, Cubic, Quart, Quint, Pow. All these are similar, only the exponent n of the function is changed – from 2 (=Quad) to 6 (=Pow). This is the following function:

For these transitions the value will first increase slowly and near the end of the effect it will grow rapidly – like the well-known parabola.

Exponential Transition

The exponential transition puts x in the exponent (along with some factors):

So the function grows even more rapidly towards the end – compared to the xⁿ-transitions.

Circular Transition

The circular transition function describes a perfect circle (in this case a quadrant):

Sinusoidal Transition

The sinusiodal transition delivers a graph which behaves like a part of a sine-curve, the result in this case is a smooth, nearly linear transition (see the graph below).

Back/Bounce/Elastic

These are special functions which use more complex formulas – have a look at the graph below to see how the back and elastic functions behave.

Back Transition

Back moves the value first in the opposite direction (in our case: the width gets smaller than 50 px) and then moves it in direction of the target value (view this in the example above).

Elastic Transition

Elastic oscillates in increasing intervals between the opposite direction and the desired one. It’s best used with ease:out or ease:in:out, otherwise it may happen that effect doesn’t reach its target value.

This transition appears like being on an elastic rope.

Bounce Transition

Bounce is the most complex function – it can’t be described as a simple formula. It first approaches the target value linear and then it oscillates between descreasing intervals, creating a bouncing effect.

Ease in and out

Ease in is the default behaviour: Here the function is applied normally.

Ease out inverts the behaviour – so the effect works backwards.

Ease in and out is more complex: In the first half of the time the transition is applied normally, in the second half it is applied reverse.

Transition functions visualized

This graph shows different transition functions (approximately):

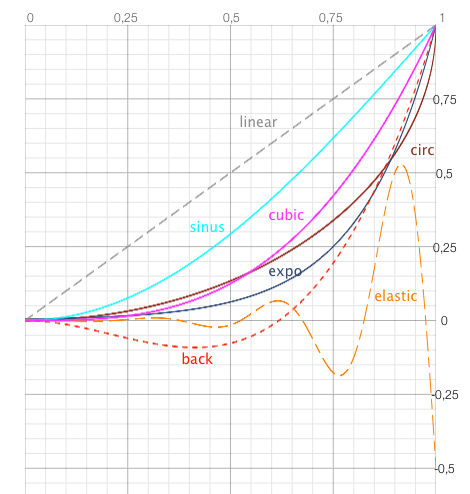
Values of transition functions

If you look at the graph above you might notice a pattern: the domain of transition functions is [0.0 ‥ 1.0] and the range is [−0.5* ‥ 1.0]. The only exception is the elastic transition and here you should use it with ease:out, otherwise the desired output might not be what you want.

* −0.5 is not a definitive value, lower values are possible — but then some unpredicted results might happen.

So generally speaking (and as nagaozen stated below) a transition function should start at (0,0) and end at (1,1).

Creating an own transition function

In case this is not sufficient, mootools offers us the possibility to apply any function as a transition. Here’s an example:

function powsin(p) {
	return (Math.pow(p + 0.4, 3) * Math.sin(p - 0.5)); // our own function
};
var transitionPowsin = new Fx.Transition(powsin);

element.set('tween', {duration: 'long', transition: transitionPowsin});

Don’t be confused by the variable “p”, it’s mootools standard in this case – you can also use “x” or whatever you like..

Now the powsin-function isn’t the most useful transition ever, but take it as an example for own experiments.

Here’s how it looks (click the pink rectangle to start):

That’s it – Comments and Feedback of course welcome.